|
|
|

|
Your CUBE BRICK puzzle set consists of 15 cubes. Each cube is different. While the whole set uses 6 colors in all, each cube has just four colors, and each four-color group occurs in only one cube. All 90 cube faces in the set are different. Each of the six faces of a cube has the same four colors as all the other faces of that cube, but in a different arrangement. The six arrangements represent all the possible ways the four color can be combined as four squares. Matching, mirror-image pairs are always on opposite faces, like this (pairs are A and B, C and D, E and F): |
|
| The goal is to join the cubes in various shapes, as shown
on the pictures and as you may create, and to match the colors between cubes
that touch. Match the colors on the faces that are up, on the top, to the
upper face colors of all neighboring cubes. Wherever two cubes meet along
an edge, the colors will flow across that edge to meet the same color on
the next cube. If the first cube (1) is placed as shown in the example below,
any cube containing green and purple can be matched to it. Let's choose
cube No. 2. It has two sides (2a and 2b), which are acceptable to match
with cube No. 1.
|
 |
| If side 2a is chosen, the third cube may be any of the cubes
with a red and orange combination. We choose, for instance, cube No. 3.
Below the first cube, we can put any cube containing red and green, like
this:
|
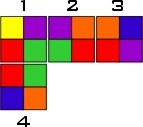 |
| Cube No. 5, to fit under cube No. 2, must match to three colors:
orange, green and red. Among the 15 cubes of the Cube Brick set, there are
always three cubes for any three-color combination. in this case, two of
those cubes have already been used and only one is available. having found
the cube with the required three colors, remember the "pairs elimination"
principle: If one face does not have the right combination, its opposite
face also will not work. turn the cube until you find the fitting pattern.
According to the same principle, you can solve even the most challenging
of the figures: the 3x5 rectangle. What we've built so far is a good start.
Now continue selecting cubes until 9 cubes form a 3x3 square, then add another
row of 3 cubes along the most convenient side, thus forming a 3x4 rectangle.
|
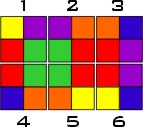 |
| With the final 3 cubes, choose the short end of the rectangle
where the cubes can fit, paying attention taht these 3 cubes have the colors
which can be matched to the 3x4 rectangle and also contain mutual colors
for matching them to each other. If, for example, the chosen side is as
shown below, and the remaining cubes are numbers 13, 14 and 15, we should
first check whether corresponding colors exist (blue/orange, orange/yellow
and yellow/blue). If so, we proceed to match their mutual colors (13 and
14 share purple; 14 and 15 share red).
|
 |
If you're missing such mutual colors, you'll need to rearrange some of the cubes you've already matched by substituting as necessary to free up the colors you need. When it's necessary to switch some cubes around from where you already matched them, first replace, if possible, only the corner cubes. Then, if necessary, change the outside ones. Try not to disturb the core of 9 cubes (3 rows by 3 coloumns) unless it's absolutely necessary.
On the following pages we show some easy fanciful fun shapes. remember that colors need to match on top wherever two cubes meet. If they meet ony along half a side, that corner must still match.
Main page ![]() Examples of solution
Examples of solution ![]() Cube Brick for kids
Cube Brick for kids ![]() How to order
How to order ![]() e-mail
e-mail